Les verres sont des matériaux omniprésents dans notre vie quotidienne. Ils proviennent de l’arrêt dynamique d’un fluide. Si un fluide est refroidi ou comprimé suffisamment rapidement, il évite la cristallisation et sa dynamique est fortement ralentie. De ce fait, le temps de relaxation, qui est une mesure du temps nécessaire à un système pour s’écouler, augmente fortement. Il est intéressant de noter que la structure globale du fluide ne change pas aussi radicalement que sa dynamique. En fait, si on compare la structure d’un système dans le régime de liquide sur-refroidi et d’un liquide dense, il serait incroyablement difficile d’identifier lequel est lequel.
Néanmoins, ces dernières années, plusieurs études montrent que certains changements dans la structure locale apparaissent dans le fluide lorsqu’il approche la phase vitreuse. Ceci ouvre la porte à plusieurs questionnements : quelles sont ces structures ? Sont-elles liées ou responsables des changements de dynamique ? Peut-on comprendre la dynamique en caractérisant simplement la structure d’un système vitreux ?
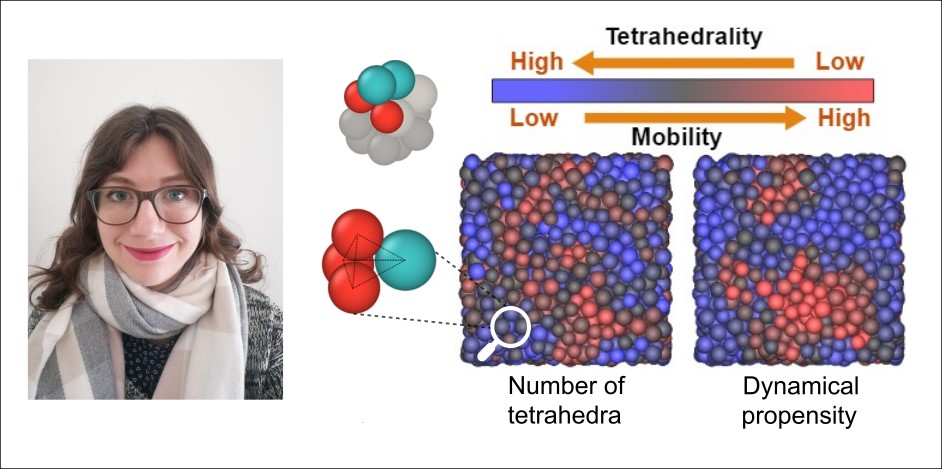
Au centre, un cluster tétraédrique typique. À droite, une image d’un mélange binaire de sphères dures. À gauche, les particules sont colorées en fonction du nombre de tétraèdres dans lesquels elles sont impliquées. Sur la droite, elles sont colorées en fonction de leur mobilité. Nous pouvons identifier que les régions rouges et bleues correspondent des deux côtés, ce qui prouve la forte corrélation entre les deux paramètres.
Ce sont quelques-unes des questions qui ont été explorées dans la thèse de Susana Marin Aguilar, qui a récemment reçu le prix Saint-Gobain édition 2020, décerné par la Société Française de Physique (SFP). La thèse a été réalisée au Laboratoire Physique des Solides (LPS) sous la direction de Giuseppe Foffi, Frank Smallenburg et Rik Wensink. Dans sa thèse, Susana a étudié l’interaction entre la structure locale et la dynamique avec des simulations de dynamique moléculaire de certains modèles de verres colloïdaux : par exemple avec des particules en patchs et des sphères dures.
En particulier, en simulant une grande variété de mélanges de sphères dures, Susana a découvert que la dynamique globale et locale de ces systèmes peut être prédite avec précision en quantifiant la tétraédricité de la structure locale : un paramètre d’ordre qui consiste à compter le nombre de tétraèdres auxquels chaque particule participe. La précision de ce paramètre est maintenue sur une grande échelle de densités prouvant son caractère universel dans cette famille précurseurs de verre.
Avec ces informations, Susana a poursuivi son travail en utilisant une méthodologie d’apprentissage automatique non supervisée (unsupervised machine learning) qui peut trouver de manière autonome des variations dans la structure locale de ces systèmes. Curieusement, ces variations structurelles sont extrêmement fortement corrélées à la dynamique future des particules. En conséquence, ces méthodes offrent une nouvelle façon de révéler la relation entre la géométrie locale et la dynamique dans les systèmes désordonnés. Cette dernière partie du travail a été réalisée en collaboration avec Emanuele Boattini et Laura Filion de l’Université d’Utrecht, et Saheli Mitra du LPS.
Références :
- Marín-Aguilar S., Wensink H. H., Foffi G., and Smallenburg F., Slowing down supercooled liquids by manipulating their local structure, Soft Matter, 15, 9886-9893, (2019).
- Marín-Aguilar S., Wensink H. H., Foffi G., and Smallenburg F., Rotational and translational dynamics in dense fluids of patchy particles, J. Chem. Phys., 152, 084501, (2020).
- Marín-Aguilar S., Wensink H. H., Foffi G., and Smallenburg F., Tetrahedrality dictates dynamics in hard sphere mixtures, Phys. Rev. Lett., 124, 208005, (2020).
- Boattini E., Marín-Aguilar S., Mitra S., Foffi G., Smallenburg F. and Filion L., Autonomously revealing hidden local structures in supercooled liquids, Nat. Commun. 11, (2020).
- Marín-Aguilar S. Smallenburg F., Sciortino F. and Foffi G., Monodisperse patchy particle glass former, J. Chem. Phys., 154, 174501, (2021).
Contact : Susana Marín Aguilar
