Unlike squares, triangles, or hexagons, pentagons cannot completely tile the plane. Using silver nanoprisms with a pentagonal cross-section, researchers have reproduced theoretically predicted tilings and determined the mechanisms that allow the transition from one structure to another.
The tiling of a plane by regular pentagons has been studied for a long time by both mathematicians as well as artists, as tilings have been used since Antiquity for artistic and decorative purposes. Thus, was raised the long-standing question of the most compact tiling using only regular pentagons. Two main tilings have particularly stood out. Firstly, a tiling found by German artist Albercht Dürer (1471-1528) assembles pentagons together by their sides to create long pentagon bands. The other tiling, named ice-ray tiling, has been proven to be the most compact tiling of pentagons, first by theoretical simulations, and more recently with a computer assisted proof.
Already observed both at the atomic and macroscopic scales, these two tilings were observed at the mesoscopic scale in a supercrystal of silver nanoprisms of pentagonal cross-section by a team of researchers from Laboratoire de Physique des Solides (CNRS/Université Paris-Saclay) and Institut Charles Sadron (CNRS/Université de Strasbourg). They also implemented an analysis method which, when joined with a model, allows to quantify the packing fraction of the experimentally obtained assemblies. Their work has been published in Nano Letters.
These two tilings were observed in crystals of a few micrometers in size, obtained by drop casting of a highly concentrated solution of nanoparticles. Moreover, since it is possible to go from one tiling to the other by a continuous sliding of the pentagons are each other, an infinity of intermediate tilings were also evidenced.Thanks to an analysis of the orientation of the pentagons in the tilings, as well as the orientation and length of their inter-center bonds, they were also able to evaluate with a high precision the packing fraction of the tiling by comparing the experimental data with data obtained from a model simulating the sliding. The presence of both phases is explained by a competition between two effects: the first one tends to maximize the packing fraction of the tiling, thus favoring the ice-ray packing, while the second effect tends to maximize the contact between the faces of the particles, and thus the edges of the pentagons, favoring the Dürer packing. This work prepares the ground for more in-depth studies on the preferential formation of either of the tilings by using surface chemistry in order to study them separately for further applications in plasmonics.
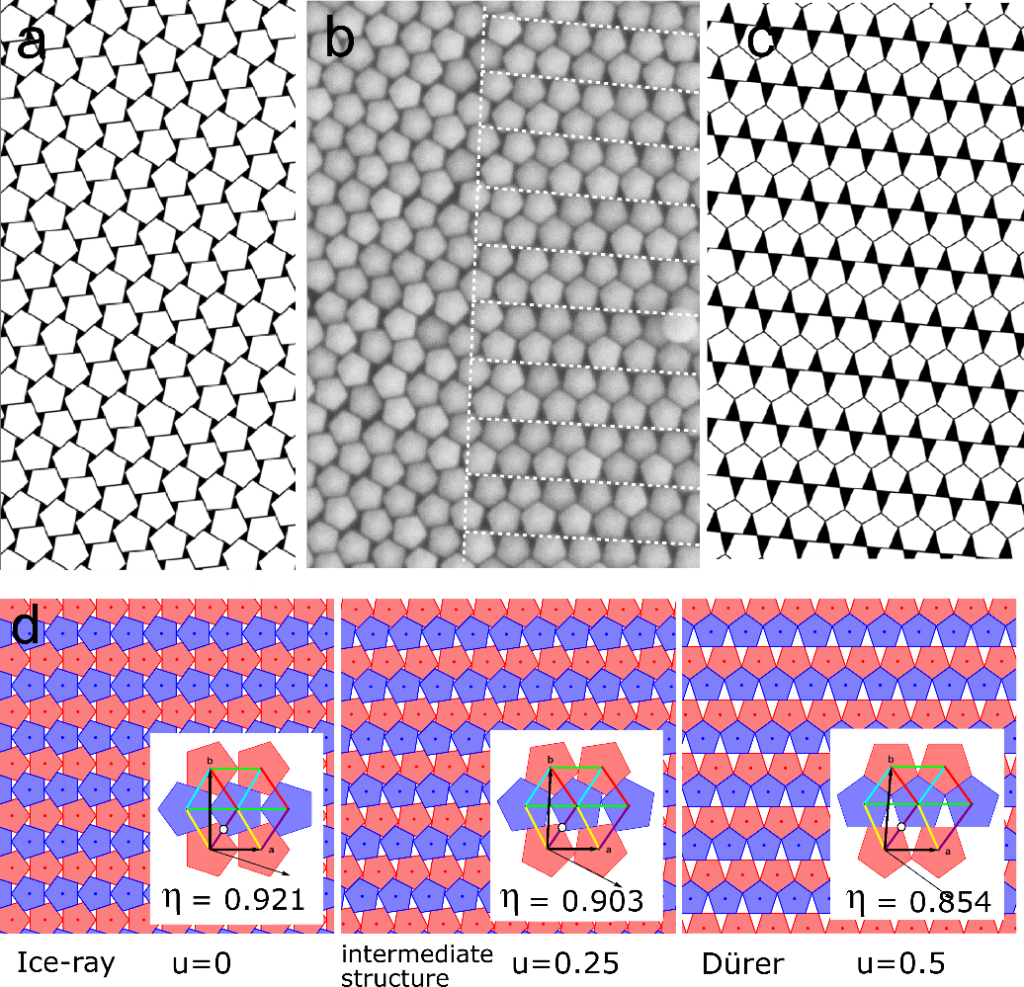
Figure. Grain boundary between an ice-ray and Dürer domain. a) Ideal ice-ray packing. b) SEM image showing an ice-ray domain on the left, and a Dürer domain on the right. c) Ideal Dürer packing. d) Scheme of the transition between the ice-ray and Dürer packing with the pentagons color-coded according to their orientation, with their matching packing fraction η and sliding parameter u, as well as a representation of their unit cell.
Reference
Polymorphous packing of pentagonal nanoprisms
J. Marcone, W. Chaâbani, C. Goldmann, M. Impéror-Clerc, D. Constantin, C. Hamon
Nano Letters, 2023, 23, 1337-1342
doi: 10.1021/acs.nanolett.2c04541
HAL Id: hal-03992796
Contacts
Jules Marcone
Marianne Impéror-Clerc
Cyrille Hamon
