The concept of topological defects plays a unifying role in condensed matter physics. Its birth, 50 years ago, was the result of interactions between specialists in crystalline dislocations, superconducting vortices, point or linear singularities in magnetism, and monopoles, disinclinations and dislocations in liquid crystals. A team of researchers has just identified a new class of defects called topological metadefects, where two or more dislocations come together and lock themselves into complex geometric arrangements.
In cholesteric liquid crystals, equipped with a helical molecular order of pitch po (Figure 1d), dislocations are particularly easy to generate by confinement in a gap between non-parallel surfaces such as the crossed cylindrical mica sheets (of radius Rm) of Figure 1a. In this geometry, where the slot thickness varies as h=hmin+r2/(2Rm), the number N of helix pitches that can be accommodated, without deviating too much from the natural pitch po, increases with radius r in increments DN=1. For this reason, in Figures 1b and 1c, fields with N, N+1, N+2, … helix pitches are separated by circular dislocations.
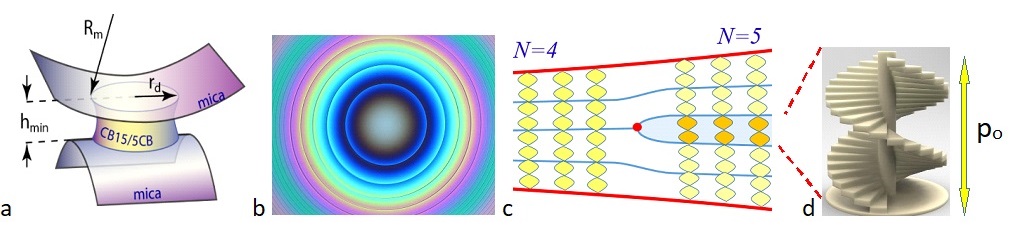
Figure 1. Dislocations in a cholesteric drop confined between two cylindrical mica sheets. a) perspective view, b) dislocations seen under the microscope, c) texture in a section perpendicular to a dislocation, N is the number of helix pitches, d) allegorical representation of the cholesteric helix of pitch po.
A team at LPS has just introduced the concept of topological metadefects, using the generic example of tangles formed by cholesteric dislocations. This work has just been published in Physical Review Letters and highlighted by the editors.
The generation of such tangles begins with the collision of two coplanar dislocations and their association to form a pair (called Lehmann cluster) of D2 symmetry (figure 2a and b). Subjected to sufficient mechanical stress (due to an increase in the distance hmin between the mica sheets), the Lehmann pair loses its coplanar configuration, the D2 symmetry Þ C2 is broken and the result is the formation of elementary twists alternately dextro- and levogyres (figure 2d). In a small cholesteric drop, a single elementary twist can be generated and then wound into a double helix (figure 2e) by the action of a continuous tensile stress.
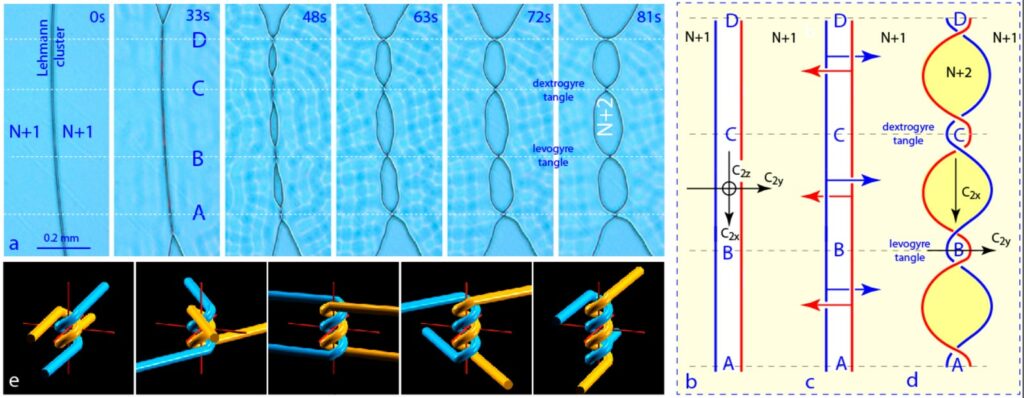
Figure 2. Generation of tangles. a) microscopic view, b) Lehmann pair of coplanar dislocations, c) dislocation movement under Peach-Koehler force due to the increase of the slot thickness hmin, d) overlapping of dislocations leads to generation of tangles.
More recent experiments have shown that, in addition to tangles, dislocations in cholesterics can also form knots (e.g. a trefoil knot) or links (e.g. a Hopf link), which are further examples of topological metadefects.
Reference
Topological metadefects : tangles of dislocations
P. Pieranski, M. Zeghal, M.H. Godinho, P. Judeinstein, R. Bouffet-Klein, B. Liagre and N. Rouger
Physical Review Letters, 2023, 131, 128101
DOI: 10.1103/PhysRevLett.131.128101
Contact
Pawel Pieranski
